Easing (or interpolation) equations are mostly used in animations to change a component value in a defined period of time.
You can move objects, change their colors, scales, rotations and anything you want simply using easing equations.
This is an example changing objects movement:
This process is often named “Tweening” and today I’d like to discover what’s under the hood and write about how to create your personal “Tween” class all by yourself.
PS. Oh hey almost three years ago I released a plugin called “Text Animator for Unity”, a tool I made/needed for my own games - and Today it is also getting used in other games like “Dredge, Cult of The Lamb”, “Slime Rancher 2” and many more!! I’d love if you could check it out! you’d also support me while I work on exciting stuff behind the scenes, so… thank you very much! ✨
Baaack to the article.
How they work
Easing functions are useful to change a value from A to B in X time, based on a mathematical function’s graph.
We’ll tweak the “percentage” parameter in the Lerp method, looking at mathematical functions that are defined in the range [0,1] (in math the square brackets mean “included” so the functions have to exist in 0 and 1 too).
We choose the range [0,1] because in our code we’ll always pass a percentage as a parameter, which represents the current time of our animation. For example if 5 of 10 seconds passed we’re going to pass “5/10“, so “0.5“. It probably seems hard at the beginning if you’re not familiar with math and so on, but I’ll talk about it step by step.
Mathematical Functions
If you don’t know what mathematical functions are here’s a really quick explanation, parallel with coding functions/methods. If you already know about them and you can jump on the Lerp section.
In our code we can have a method named “f”:
float f(float x){
return x+4;
}
In math , we have “f(x) = x+4”.
This means that f(6) = 6+4 = 10, or f(0) = 0+4 = 4.
The same value is returned by our method written above, if we give the same parameter.
“f” is the name of the function, could be “g” “h” or whatever you want. Just like our method names.
X is a placeholder, and it’s replaced by a value that you give. Just like parameters/variables in our codes.
After the “=” we have an equation, that returns a value based on the “x” that we give, just like inside our method.
Also, f(x) = x+4 or y=x+4 are the same thing.
A function defines how a set of input values correspond to a set of output values. One input can return only one output.
Function’s Graph
To display this input-output relation we can use a (2D) cartesian coordinate system. At each X (input) corresponds a Y (output).
In our case we’re always using the example f(x) = x+4.
We can calculate a few points, such as f(-4) = 0, f(-2) = 2, f(0) = 4, f(2) = 6, and later we can connect them.
On the “X” axis we go on the value “-4” and draw a point (y=0). Then we go on the X value “-2”, go upper of 2 units (this way we go on the Y value “2” ) and we draw another point. After drawing all these points we can see that this is is a linear function and its graph is:
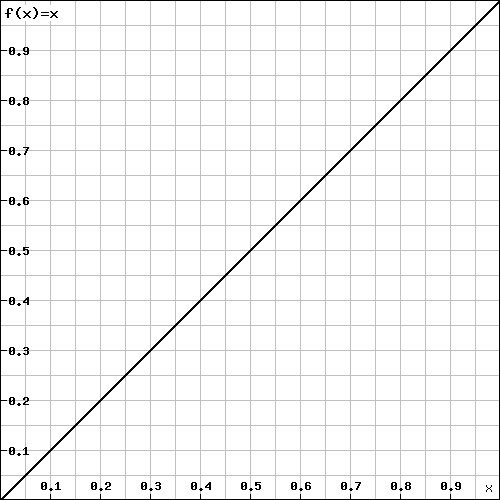
Of course, a computer draws all the points perfectly thanks to an algorithm, we can’t draw non-linear functions using this method (we’ll need derivatives, we’ll have to study the domain, the symmetries, the sign and so on), but that’s still useful to understand how drawing a function works without going deeper.
Tip: You can use any website that draws the graph of a function to follow up here, without having to calculate each point and more complex things.
Now that we know what mathematical functions are and how to draw and represent them, we can go forward with the “Lerp method”.
Lerp
The method named “Lerp” stands for “Linear interpolation” and has always 3 parameters, a “start value“, an “end value” and a “percentage” (our current progress).
It’s useful to tweak a value “from point A to point B” based on the percentage (progress) parameter that you give.
Example: If we want to go from 0 to 4 and give 0.5 as percentage value, we’ll get 2 from this method (our middle value). If we give 0 we’ll get the start value and if we give 1 we’ll get the end value.
/// <summary>
/// Linearly interpolates a value between two floats
/// </summary>
/// <param name="start_value">Start value</param>
/// <param name="end_value">End value</param>
/// <param name="pct">Our progress or percentage. [0,1]</param>
/// <returns>Interpolated value between two floats</returns>
static float Lerp(float start_value, float end_value, float pct)
{
return (start_value + (end_value - start_value) * pct);
}
In Unity the method Mathf.Lerp is already written and ready to use.
Mathf.Lerp Documentation.
Lerp for Structs
We can implement Lerp for our custom structs in mainly two different ways (I’m using the Vector3 struct as an example):
//This is the same as Unity's "Vector3.Lerp"
public Vector3 Lerp(Vector3 start_value, Vector3 end_value, float t)
{
t = Mathf.Clamp01(t); //assures that the given parameter "t" is between 0 and 1
return new Vector3(
start_value.x + (end_value.x - start_value.x) * t,
start_value.y + (end_value.y - start_value.y) * t,
start_value.z + (end_value.z - start_value.z) * t
);
}
//This is the same as Unity's Vector3.LerpUnclamped
public Vector3 LerpUnclamped(Vector3 start_value, Vector3 end_value, float t)
{
return new Vector3(
start_value.x + (end_value.x - start_value.x) * t,
start_value.y + (end_value.y - start_value.y) * t,
start_value.z + (end_value.z - start_value.z) * t
);
}
As you can see, the main logic is to lerp each value individually, choosing between a LerpUnclamped and a Lerp.
As said before, the percentage value “t” is always between the range [0,1]. (0.00f means 0%, 0.50f means 50% and 1.00f means 100%), and Lerp assures that the value is within the range.
Documentation: Vector3.Lerp, Vector3.LerpUnclamped, Math.Clamp01.
Animating Components
Now that we know about Lerp, we’d need a short code to see our progress! I’ll add a ball that moves from (0,0) to (0,1) in 1 second, but you can change whatever value you want! Light intensity, rotation, scale, color [….]
An abstract fragment of our code could be like this (to let you understand the logic):
float time = 0; //Current time or progress
float duration = 4; //Animation time
while(time<=duration) //inside this loop until the time expires
{
object.position.y = Lerp(0, 1, time/duration); //Interpolates the object's "y" value from 0 to 1
//Wait 1 millisecond, depends on your language
time += 1; //Adds one millisecond to the elapsed time
}
In Unity we can write a Coroutine:
/// <summary>
/// Changes the object's position "y" value in X time
/// </summary>
/// <param name="transform">The object's transform</param>
/// <param name="y_target">"Y" target coordinate</param>
/// <param name="duration">The duration of the interpolation</param>
/// <returns></returns>
public static IEnumerator ChangeObjectYPos(Transform transform, float y_target, float duration)
{
float elapsed_time = 0; //Elapsed time
Vector3 pos = transform.position; //Start object's position
float y_start = pos.y; //Start "y" value
while (elapsed_time <= duration) //Inside the loop until the time expires
{
pos.y = Mathf.Lerp(y_start, y_target, elapsed_time / duration); //Changes and interpolates the position's "y" value
transform.position = pos;//Changes the object's position
yield return null; //Waits/skips one frame
elapsed_time += Time.deltaTime; //Adds to the elapsed time the amount of time needed to skip/wait one frame
}
}
Here is this algorithm’s visualization:
You can see that the object’s Y coordinate goes from 0 to 1 directly, starting with a constant speed until the end of the animation. As the name says: Linear interpolation.
As you can imagine, with little implementation you can apply an interpolation on any component you want.
Ease In
Now it’s the moment to play with math a bit, we just need to ask ourselves: what if we want to launch a rocket? Since rockets need time to accelerate, using the linear interpolation would be unrealistic. Can you imagine a rocket going up with a constant velocity directly from the launch? “0/10 physics engine broken”, someone would say.
Initially we need to find a mathematical function that “starts slowly“.
The “exponential” one (x*x) is what we need and the result is the following:
This “easing function” or “interpolation/tween type” is mostly called “EaseIn“, since it starts slow. You’ll see sometimes the name “SmoothStart” , which gives the same idea.
public static float EaseIn(float t)
{
return t * t;
}
In our previous abstract fragment code we can now place this function:
object.position.y = Lerp(0, 1, EaseIn(time/duration));
or here in our Unity’s Coroutine:
pos.y = Mathf.Lerp(y_start, y_target, EaseIn(elapsed_time / duration));
You can then hit play and see the difference! Our imaginary rocket-fans would be proud of us.
The more times you elevate the “t”, the slower our component’s value will start.
Now that we know the overall concept we can start playing with functions even more.
Flip
The code to flip a function is the following:
static float Flip(float x)
{
return 1 - x;
}
Exponentials
With exponentials (x^y) I suggest to avoid placing a big loop in an function or even a recursion (like the function pow), since it could require a lot of resources in some hardwares. Consider writing suggest to write single easing functions and name them with their power value instead, such as “EaseInQuadratic” will have an “xx“. “EaseInCubic” will have “xx*x” and so on.
Ease Out
What if we want to show a rocket’s landing? Since our rocket decelerates while landing we need the opposite of EaseIn.
We could take the EaseIn graph and flip it, obtaining this:
The function now is slower at the end but we want it to start from 0 and reach 1, otherwise it will work inversely as intended. We can flip the progress inside the power, having this as the result:
That’s it! Now our object is slower at the end, which means that our rocket will reach its destination decelerating!
P.S. Dont be distracted because the ball is going up, it only means that it’s reaching the destination. Do you remember? if the percentage is 1 it means that we reached our end point (which is up in this example). If you set the target destination below the object it will go down.
The EaseOut function is the following:
public static float EaseOut(float t)
{
return Flip(Square(Flip(t)));
}
This is the result if we elevate the progress in three different ways:
Ease In Out
What if we want our rocket to start AND land using the same easing function? Well, we need it to start accelerating (EaseIn) and stop decelerating (EaseOut), creating a EaseInOut. We need to “use the last function the nearest we are with the end”….we need a Lerp!
The EaseInOut function is the following:
public static float EaseInOut(float t)
{
return Lerp(EaseIn(t), EaseOut(t), t);
}
The more we progress the less we’ll use EaseIn.
Spike
“Mirrored” easing functions are mostly used for “UI” animations, since they reach their destination and then they go back at their initial state.<hr> You can imagine a “pop up“, a click on a button that increases its size and then resets it, […].
I like to call it “Spike” because its graph reminds me it and also because you can easily move a spike in a game using this!
We start with an EaseIn but this time we need to reach 1 when 50% of the time elapsed. This means adding a simple if condition to our code and divide by 0.5f.
public static float Spike(float t)
{
if (t <= .5f)
return EaseIn(t / .5f);
//Step 2
}
When we’ve reached .5f we need the opposite and reach the start again. We need to “mirror” the EaseIn, so we’ll use it again but in reverse.
Our (final) code is the following:
public static float Spike(float t)
{
if (t <= .5f)
return EaseIn(t / .5f);
return EaseIn(Flip(t)/.5f);
}
In the image I showed earlier I used “Spike2“, where I raised the parameter given in each EaseIn to a power of 2.
More of them!
Now that you know a lot of basic functions, play with them!
Here are my references: Robert Penner’s easing functions, http://gizma.com/easing/ (to look at some functions), https://gist.github.com/Fonserbc/3d31a25e87fdaa541ddf (to look at other functions).
I experimented a bit and here’s the result:
I also suggest this GDC Video: Math for Game Programmers: Fast and Funky 1D Nonlinear Transformations, where you can also have another explanation on easing functions.


